Simpson’s paradox：辛普森悖論與隱藏變因

分類：seaturtlecareers發表於職場即戰力標籤：，，，，，

Paradox 翻譯為『悖論』， 指的是『似非而是』：也就是那些看起來很奇怪，但是仔細想想道理是正確的現象。辛普森悖論指的是『整體趨勢與個別趨勢不同』的現象。本篇我們從辛普森悖論出發，探討這種現象成因，以及資料分析中常見的謬誤。

辛普森悖論，最經典的案例之一，是 1973 年加州大學柏克萊分校的性別錄取比例。

整體看來，女學生的錄取率比男學生要低，但是如果分不同學院比較，大部分的學院中，女學生的錄取率都是較高的。造成這個現象的原因，是因為較多女性申請『錄取率低的學院』。

辛普森悖論的成因

了解辛普森悖論，最重要的教訓是『不要把現象上的相關當作是因果關係』。

隱藏變因

隱藏變因（lurking variables）指的是在我們只看到 A → B 的關係時，忽略了另一個變因 C 的作用。

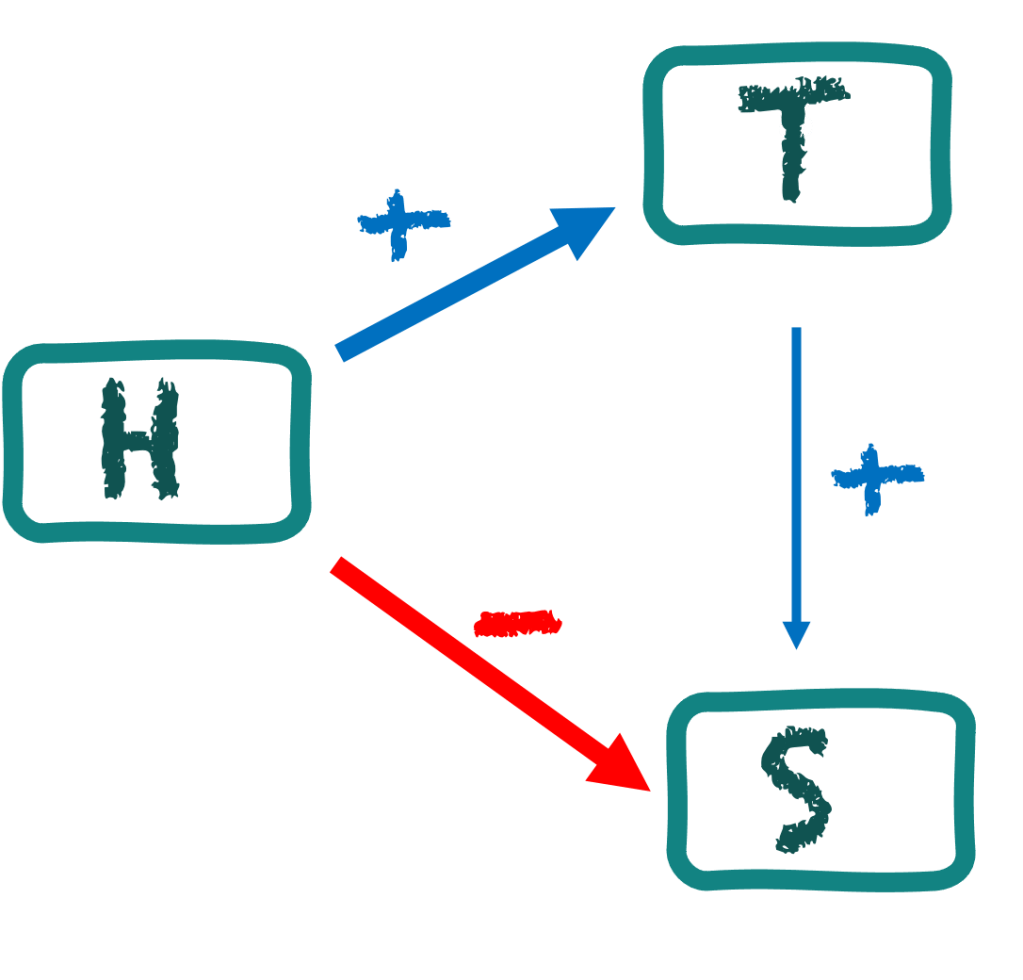
例如前面性別錄取比例的例子，真正的模型是：性別 → 申請學院比例 → 錄取率 (Gender, College, Admission)。但是當我們忽略中間的 『申請學院比例』時，就可能會產生錯誤的結論。即使實際上，每個學院對女性的錄取率較高（G –> A 的小藍色箭頭），在現象上會辦間接的負相關蓋過。

(性別 Gender, 學院的整體錄取率 College, 錄取率 Admission 的結構模型)

另一種隱藏變因是 C 同時影響了 A 和 B

例如：整體看來，所有受僱用者一年休假的時間越多，隔一年升職加薪的機率越高；而如果按照行業，職位等等區分，這個關係可能不存在甚至相反。可能的解釋是，因為越賺錢，（或是越有前途的工作，越有良心的老闆），越願意讓員工休假，也更能提供升職加薪的機會。

(工作的好壞 Job, 放假的天數 Vacation, 加薪的機率 Raise 的結構模型)

#這個例子是從一篇 HBR 文章：放假天數與加薪的關係聯想而來。
#這篇本來是想用來做『data driven』的例子，但是不能驗證數據是否有道理，是否存在可能的辛普森悖論，所以放在這裡作參考。文章還是可以一看：總體而言，『有假不放未必對個人職涯發展有什麼好處』這個結論應該還是對的。

另一個經典的案例，是『學習時間與考試成績的關係』。

整體現象顯示，學生花在學習的時間，與考試成績成反比，然而如果將資料按照『學科』區分，就會發現對於每個學科，學習時間越長，其實成績會越好。

這是以簡易的 path model 數據模擬出來的圖，歡迎聯絡我們索取 python 原始碼

這裡隱藏的變因可以說是『學科難度』：難度越高，學生花在上面的時間越長，難度越高，成績也會越差，因此即使學習時間越長成績會有提升，只看整體現象時會得到相反結果。

(學科難度 Hardness、 學習時間 study Time、 和分數 Score 的模型)

如何看待『辛普森悖論』

辛普森悖論本身不是錯誤，而是複雜的系統所產生的有趣的現象，更可以是分析師科學家可遇不可求的『洞見』（insights）。

因果措置和隱藏變因不一定會產生辛普森悖論，但是如果看到類似 辛普森悖論的現象，就要重新檢視思維模型，是否有漏掉重要因素或是錯誤歸因的可能。

另外，雖然我們通常著重於有因果關係的推論（例如女性是否在入學率上遭受歧視，多休假是否會造成少加薪），但是那個『相悖』的大趨勢，其實也是真實不容忽視的現象（女性總體入學率低，放假與加薪呈現相反關係仍然是事實）。

歸根結底，在分析數據時，要多做探索與視覺化，也要有 business sense 和常理推斷，建立思維模型，才能區分『現象』與『根本原因』。對現象正確的解讀，不是只是數據分析師的基本功，不管什麼崗位，工作中都要有能明辨是非的能力，生活中也可以減少被騙、吃虧上當的可能性。