一般人在分析任何資料，都會關注相關性（correlation）。字體大小與點擊率的關係，西瓜敲起來聲音脆不脆與好不好吃的關係，小朋友睡眠時間與身高的關係。相關性本身是了解系統運作的重要參考，但是如果把相關性誤認為因果關係，就會造成錯誤的結論。

---

共同原因，間接影響

忽略隱藏的變因，是造成錯誤歸因的一個常見的機制。複雜系統中，間接的因果關係，也會產生觀察到的『相關性』。如果沒有對系統的正確認知，就很容易把相關性誤認為因果。

最簡單的系統模型，有共同原因和間接影響兩種。

共同原因

假如變因 Ａ 同時影響了B 與 C，即使 B 與 C 本身沒有任何因果關係，也會產生相關的現象。

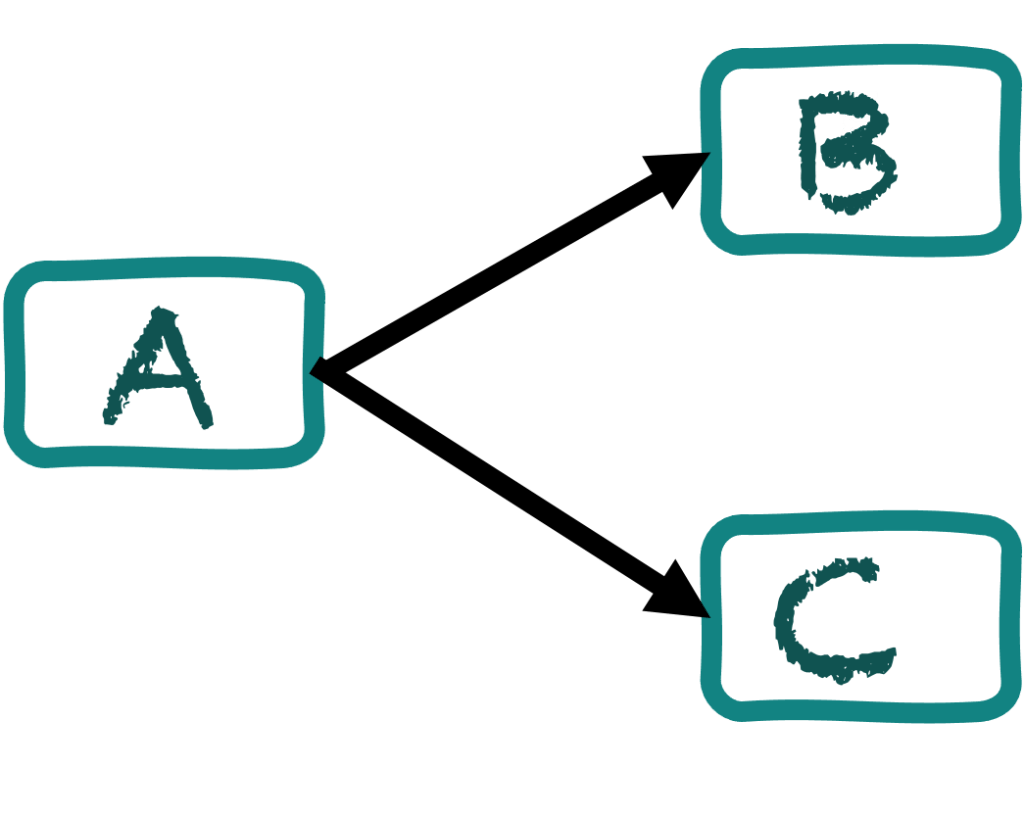
間接影響

假如變因 Ａ 影響 B，B 又影響 C，那麼 A 和 C 之間即使沒有直接影響，也會有相關性。

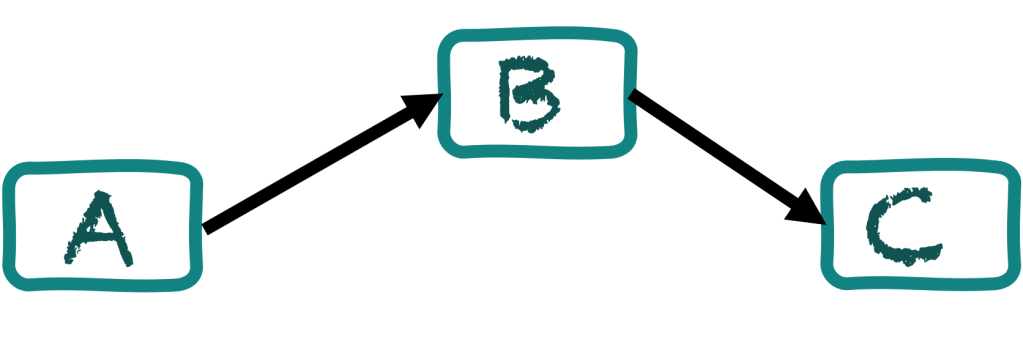
隱藏變因可能會造成『辛普森悖論』等等特別的現象。上述兩種簡單模型，數據處理上可以用 partial correlation，殘差分析之類的方法適當排除隱藏變因的影響。

互為因果的變因：回饋

回饋（feedback）或稱反饋，是自然界和人類世界都非常常見的一種機制。指的是兩個變因互相影響。例如：業績好，就減少宣傳力度，不宣傳，業績又會變差。這種機制相反的回饋稱為『負回饋』（negative feedback）。

另一種案例：成績好，讓人喜歡學習，喜歡學習成績又變得更好。這種就叫做『正回饋』（positive feedback）。

從資料分析與洞見的角度而言，再負回饋的系統中，如果不能釐清反饋的機制，只就現象進行分析，可能會造成『因果錯置』，或稱為『倒果為因』的錯誤結論。

舉另一個假想的例子：

如果我們看到買豪車的人，通常也比較有錢，而推斷『買豪車』會讓人變『有錢』，這就是錯誤的推論。其實是『有錢』的人比較會『買豪車』(圖示以 L 代表 Luxurious car)。(而買豪車本身其實是會讓人變窮一點點的)

用時間序列研究回饋機制

如果只做簡單的相關性分析，幾乎不能拆解回饋系統中的因果關係。除了實驗或類似實驗的方法外，可以從時間序列分析下手。因果關係的基本原理之一，是『因』一定發生在『果』之前。

簡單的交叉回歸（cross correlation），或是以值對『差值』（difference）的交叉回歸，可能可以找出兩個變因之間互相的影響力。在單一時間序列中，如果發現自我相關（autocorrelation）也表示有回饋機制存在的可能。

複雜系統與結構模型 SEM 

我們以上介紹的幾個系統，其實都是相當簡化的模型。真實世界其實是非常複雜的，但是在研究與資料分析時，必須要適當的簡化，並且假設你的模型就是個相對獨立的系統。如同我們前面的幾個圖示，複雜系統也可以用『變因』與『影響力』畫出模型。

這種模型也可以稱為路徑模型（path model）。假設系統中的影響力可以用類似回歸分析的方式呈現，也可以稱為結構（方程）模型（Structural Equation Model; SEM）。

實驗之外的方法：『類實驗』分析

探討因果關係最有力的方法還是實驗，但是實驗的成本太高，甚至有時候根本不可行。

另一種方法是尋找『類似實驗效果的資料分析』，可以稱為『類實驗』：包含中斷時間序列 (interrupted time-series)，與合成控制組（synthetic control）等方法。

前述結構模型可作為驗證因果關係的最後手段。所有變因相關性（以 correlation matrix 呈現）也可以用來驗證特定的結構模型。這種分析叫做結構方程分析（Structural Equation Modeling）。然而，因為結構方程分析是將提出的模型當作 null hypothesis 來驗證，所以其威力（power）有限，只能作為輔助或是最後的手段。

---

『相關性不代表因果關係』

做資料分析或是審閱 data driven projects 時，一定要謹慎判別，多加探索。更重要的，是要對要研究系統有深入的，實際的了解，不能侷限於現有的資料（錯誤的資料無論怎麼分析都得不到正確的結論）。要用 business sense（很多時候是 common sense）找出可能的隱藏變因，對結構模型有基本的假設，才能得到更接近真實機制的結論。